Unit 5 comparing linear quadratic and exponential functions answer key – Unit 5: Comparing Linear, Quadratic, and Exponential Functions Answer Key provides a comprehensive overview of the key characteristics, equations, and applications of these three fundamental function types. This guide offers a thorough understanding of the concepts and their practical relevance in various fields.
By delving into the intricacies of linear, quadratic, and exponential functions, this answer key empowers students to analyze and solve real-world problems effectively. It serves as an invaluable resource for solidifying the understanding gained in Unit 5, enhancing problem-solving skills, and fostering a deeper appreciation for the power of mathematical functions.
Comparing Linear, Quadratic, and Exponential Functions: Unit 5 Comparing Linear Quadratic And Exponential Functions Answer Key

Linear, quadratic, and exponential functions are three fundamental types of functions commonly used in mathematics and various fields. Understanding their characteristics and differences is crucial for solving problems, making predictions, and modeling real-world phenomena.
1. Linear Functions
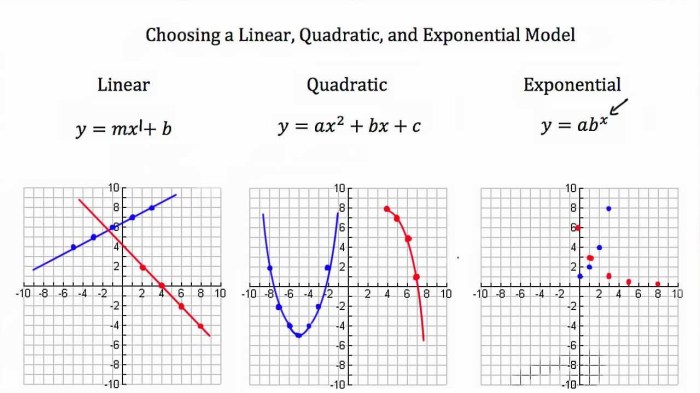
Linear functions represent a straight line on a graph. They have a constant rate of change and can be expressed in the form y = mx + b, where m is the slope and b is the y-intercept.
- Equation form: y = mx + b
- Graph shape: Straight line
- Slope: m (constant rate of change)
- Y-intercept: b (where the line crosses the y-axis)
- Real-world examples: Population growth over time, temperature change with altitude
2. Quadratic Functions, Unit 5 comparing linear quadratic and exponential functions answer key
Quadratic functions are characterized by their parabolic shape on a graph. They can be expressed in the form y = ax² + bx + c, where a, b, and c are constants.
- Equation form: y = ax² + bx + c
- Graph shape: Parabola
- Vertex: (h, k), where h = -b/2a and k = f(h)
- Axis of symmetry: x = h
- Real-world examples: Projectile motion, parabolic flight of objects
3. Exponential Functions
Exponential functions represent exponential growth or decay and are expressed in the form y = a(b)^x, where a is the initial value, b is the base (growth rate), and x is the independent variable.
- Equation form: y = a(b)^x
- Graph shape: Curve
- Base: b (growth rate)
- Real-world examples: Population growth with unlimited resources, radioactive decay
4. Comparing Linear, Quadratic, and Exponential Functions
| Function Type | Equation Form | Graph Shape | Real-World Examples |
|---|---|---|---|
| Linear | y = mx + b | Straight line | Population growth, temperature change |
| Quadratic | y = ax² + bx + c | Parabola | Projectile motion, parabolic flight |
| Exponential | y = a(b)^x | Curve | Population growth, radioactive decay |
5. Applications of Linear, Quadratic, and Exponential Functions
These functions have numerous applications in various fields:
- Linear functions:Modeling population growth, predicting weather patterns, calculating distances
- Quadratic functions:Designing parabolic antennas, optimizing trajectories of projectiles, analyzing projectile motion
- Exponential functions:Describing radioactive decay, modeling population growth with unlimited resources, predicting the spread of epidemics
6. Practice Problems
Solve the following problems:
- Find the slope and y-intercept of the linear function y = 2x
5.
- Determine the vertex of the quadratic function y = x²
4x + 3.
- Find the base and growth rate of the exponential function y = 100(1.05)^x.
Question & Answer Hub
What are the key differences between linear, quadratic, and exponential functions?
Linear functions have a constant rate of change, quadratic functions have a parabolic shape, and exponential functions have a constant growth rate.
How can I identify the type of function from its equation?
Linear functions have an equation of the form y = mx + b, quadratic functions have an equation of the form y = ax^2 + bx + c, and exponential functions have an equation of the form y = a^x.
What are some real-world examples of linear, quadratic, and exponential functions?
Linear functions can be used to model population growth, quadratic functions can be used to model projectile motion, and exponential functions can be used to model radioactive decay.